一維流動的質量守恒
首先來看一下一維流動中的質量守恒,質量守恒決定了,在流動中任意流體微團的質量都應該保持不變。數學表達式是這樣的: 其中質量與密度和體積的乘積來表示。因為在流體力學中,通常用來表示速度,這里用B來表示體積。很顯然,這種表達式是拉格朗日方法,是針對一個流體微團的。
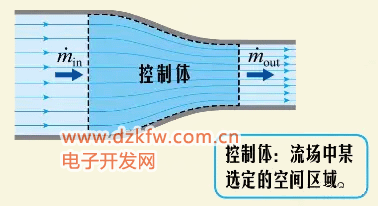
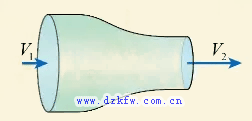
現在來看看流體力學的歐拉法中的質量守恒。在這樣一個一維流動中,取中間一段作為控制體流體,從左邊流入右邊流出。
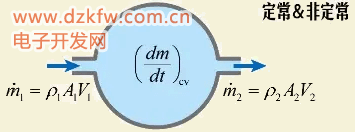
根據質量守恒可知,控制體內質量的增加等于流入的質量減去流出的質量 這就是質量守恒在歐拉法中的表現形式。 當流動為定常時,控制體內的質量保持不變,于是可知,任意時刻流入控制體的質量等于流出控制體的質量:
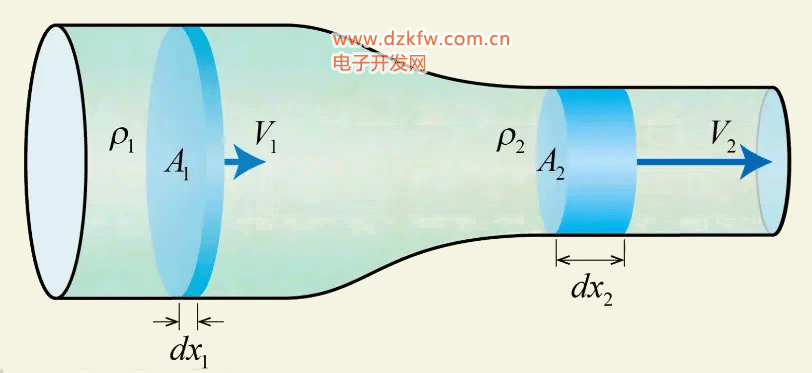
這里的m表示了單位時間流過的質量,稱為流量。我們通過這樣一個圖來看看流量與流速的關系。對于定常流動單位時間流過進口和出口截面的質量相等,質量等于密度與體積的乘積。在直徑大和直徑小的地方,同樣體積的流體所占流向長度是不同的,這個流向長度與時間的比值就是當地的流速。于是我們就得出了流量的表達式:通過橫截面的質量流量等于密度、橫截面積和流速三者的乘積,而體積流量等于橫截面積和流速的乘積。
質量守恒在流體力學中體現為流量連續,所以稱為連續方程: 當流動為不可壓縮時,密度不變,連續方程可以表示為:
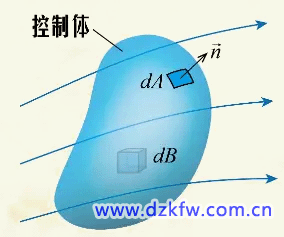
連續方程的一般形式現在來看看連續方程的一般形式。既三維復雜流動中的質量守恒,在流場中取這樣一個任意的控制體,其表面稱為控制面: 根據質量守恒,單位時間控制體內質量的減少,應該等于流出控制體的質量。于是我們可以寫出連續方程的積分形式的表達式:
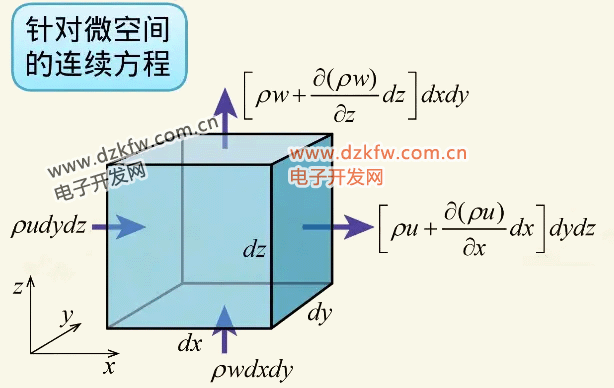
這種積分形式適用于做理論分析,如果要具體計算流場參數需要用到微分形式,所以我們現在來針對微小的控制體推導連續方程。取這樣一個六面體為控制體。
在六個面上流體可以流入和流出在左側面和下側面上進入的流量表達式為 而右側面和上側面上流量的表達式用相應的一階泰勒展開表示: 由于控制體體積不變,控制體內單位時間質量減少就體現為密度的減少: 而根據圖中所示,左右兩個側面上的流量之差是凈流出的質量: 于是,我們可以得到所有六個面上的凈流出量: 質量的減少等于凈流出量,于是就可以得出我們所需要的關系是: 體積項 可以消去,就得到連續方程的表達式: 這個表達式是分量形式的,可以簡化寫成矢量形式: 其中的 是拉普拉斯算子,而 稱為密流,即單位面積的流量。
連續方程的分析與應用現在我們來分析一下連續方程在具體應用時的特點。首先,這個方程的第一項表示了控制體內密度的變化,當流動為定常時,這一項應該為零。于是我們得到定常流動的連續方程,即密流的散度為零: 進一步可以得到一維定常流動的連續方程:當流動維不可壓時,得到一維定常不可壓流動的連續方程: 也就是說,一維定常不可壓流動中流速沿流向保持不變。可是這個推導是不是有問題呢?很顯然。對于因為收縮通道內的流速沿流向是增加的。
這個推導是看不出問題的。其實,問題在于收縮通道的流動不是一維流動。在工程上把它當作一維流動處理,把另外兩位的速度變化用面積變化來表現了。
從連續方程還可以進行這樣的變換,把對密度和速度的微分展開成兩項: 可以看出。這個式前兩項是密度的隨體導數,而連續方程可以寫成這樣: 因為全導數表示的是流體微團密度的變化,所以這是拉格朗日法的連續方程。這種形式的聯系方程的物理意義也是很明確的,流體微團的質量變化可以認為有密度和體積兩種因素,這個連續方程里面的第一項表示了密度的變化,第二項表示了體積的變化。由于流體微團質量保持不變,所以密度增加,體積必然減小,反之亦然。
從拉格朗日法的連續方程還可以得出,不可壓縮流動的連續方程,就是速度的散度為零: 物理意義是流體微團的體積變化為零。
我們再來看一下,所謂因為收縮通道的流動,這次加上不可壓的條件來分析收縮通道中部一點處的速度變化情況。
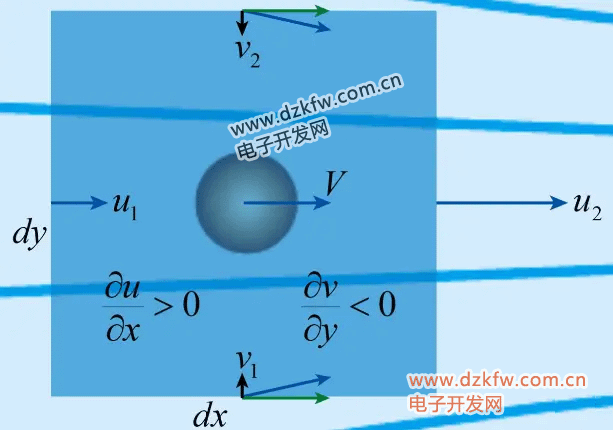
在這一點的鄰域取一個微小的控制體,其上下左右各面的速度如圖所示。左右側面只有x方向的速度,右側面的速度比左側面大,上下表面速度的x分量相同,y分量大小相等方向相反。于是可知u沿x方向是增加的,而v沿y方向是減小的。
把二維不可壓連續方程寫出來: 可以看出和流場分析是一致的,這兩項的符號必然相反,而且大小應該相等。從這里我們可以看出x方向速度的增加,伴隨著y方向速度的減小,所以收縮流動至少是二維的,而不可能是一維的。
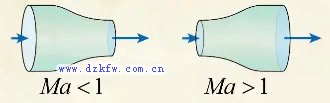
現在來看看壓縮性的影響,當流動為可壓縮時,連續方程中的密度會改變,低速流動中的密度的變化相對較小,因此收縮就加速在定性上總是正確的。當氣體以超音速流動時,密度的變化很大,比速度的變化量還要大,也就是說這時速度增加一倍,密度會減小的比一半還小,所以面積以速度的關系就反過來了。超音速氣流通過擴張通道時才會加速。
歷史上,瑞典工程師拉瓦爾在研究沖擊式渦輪的時候,采用收縮擴張的管道,成功讓氣流從亞音速加速到了超音速。于是,這種管道就被稱為拉瓦爾噴管。
再來看看不可壓和非定常的關系。這是不可壓連續方程: 在推到它時,并沒有假設定常流動。所以這個三維方程包括它的一維形式,對定常和非定常都成立的。
比如這個模型中,不可壓時,流體密度不變,所以容腔內的流體質量保持不變,于是可知那一瞬間進出口的流量相等,可以說,單看總流量的話不可壓縮流動只能是定常的。
接下來我們看一個流動的例子,假設有一輛行駛中的汽車缺了一塊玻璃,而其余各處密封都完好不漏氣。
分前窗側,窗和后窗三種情況來考慮。空氣是流進來還是流出去?從經驗判斷,前窗缺玻璃時,氣體流入;后窗缺玻璃時氣體流出。是這樣嗎?汽車的運動速度不高,屬于不可壓縮流動,可以用不可壓縮連續方程來判斷這個問題。只有一個開口,無論開口朝什么方向,流體都應該是不進也不出。雖然這似乎和感覺不同,但這就是連續方程給出的結果。那為什么坐在窗子邊會有很大的風吹進來呢?這其實是流動的非定常性造成的,因為非定常性缺口有可能一半流出一半流入。
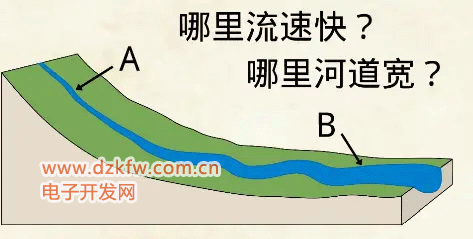
我們再來看一個河流的例子。假設這是一條沒有支流的河上游,坡度大,下游坡都想那么在圖中的A點和B點哪里流速快呢?這個很好判斷坡度大的地方流速快。那么哪里河道寬呢?
這個可以用連續方程來判斷流速小的地方需要的橫截面積大,一般河面會寬。所以在這個例子中,流體的橫截面積是由流體速度決定的。
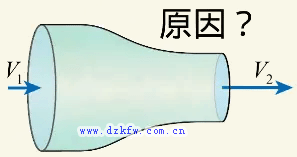
對于封閉管道內的流動橫截面積是由管道決定的。看來似乎面積的收縮是流體加速的原因了。
然而很顯然,流體遵從牛頓定律加速一定是受到了驅動力的作用。粗的地方壓力高,細的地方壓力低。流體微團流經收縮通道時,是從壓力高的地方流向壓力低的地方,相當于微團背后的壓力大于前胸的壓力,被推著加速前進,這就是驅動力了。所以流體加速是壓力差的驅動造成的。






 返回頂部
返回頂部 刷新頁面
刷新頁面 下到頁底
下到頁底